ANOVA 분석: 일원 & 이원 (예제 포함)

분산분석(ANOVA)

분산 분석(ANOVA)은 두 개 이상의 그룹 평균 간의 차이를 검정하는 데 도움이 된다. 분산 분석 시험은 일반적인 변수에서 다른 변동 소스(군간 및 군내 변동)를 중심으로 한다. 주로 분산 분석 검정은 그룹 간 평균이 같은지에 대한 증거를 제공한다. 이 통계적 방법은 t-검정의 연장이다. 요인 변수가 두 개 이상의 그룹을 갖는 상황에서 사용된다.

이 튜토리얼에서는다음에 대하여 학습한다.

일원 ANOVA

There are many situations where you need to compare the mean between multiple groups. For instance, the marketing department wants to know if three teams have the same sales performance.

Team: 3 level factor: A, B, and C
Sale: A measure of performance

여러 그룹 간의 평균을 비교할 필요가 있는 상황이 많다. 예를 들어, 마케팅 부서는 세 팀이 같은 판매 실적을 가지고 있는지 알고 싶어한다.

팀 : 3 수준 factor : A, B, C
매출 : 실적척도

분산 분석 검정은 세 그룹이 유사한 성과를 가지고 있는지 여부를 알 수 있다.

데이터가 동일한 모집단에서 나왔는지 여부를 명확히 하기 위해 일원 분산 분석(one-way analysis of variance(이후 일원 ANOVA)을 수행할 수 있다. 이 검정은 다른 통계적 검정과 마찬가지로 H₀ 가설을 승인할 수 있는지 또는 거절할 수 있는지 여부를 입증한다.

일원 ANOVA 검정의 가설:

H₀: 그룹 간 평균이 동일함
H₁ : 적어도 한 집단의 평균은 다르다.

즉, H₀ 가설은 집단(factor)의 평균이 다른 집단의 평균과 다르다는 것을 증명할 충분한 증거가 없다는 것을 암시한다.

2개 이상의 그룹이 있는 상황에서는 분산 분석 검정이 권장되지만 이 검정은 t-검정과 유사하다. 이를 제외하고 t-검정과 분산 분석은 유사한 결과를 제공한다.

가정

우리는 각 요인이 무작위로 표본 추출되고 독립적이며, 값은 모르지만 동일한 분산을 가진 정규 분포 모집단에서 나온다고 가정한다.

ANOVA 검정의 해석

F-통계량은 데이터가 상당히 다른 모집단, 즉 다른 표본 평균에서 나왔는지 여부를 검정하는 데 사용된다.

F-통계량은 그룹간 변동성(between group variation)을 그룹내 변동성(within group variation)으로 나누어서 계산한다.

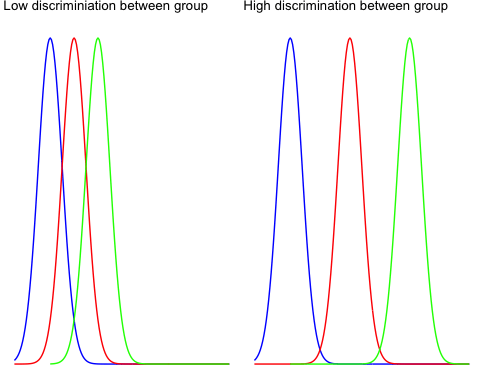
그룹간 변동성은 모든 모집단 내부의 그룹 간의 차이를 반영한다. 그룹 간 분산 개념을 설명하는 아래 두 그래프를 보기 바란다.

'왼쪽 그래프'는 세 그룹 간에 차이가 거의 없으며, 세 가지 평균이 전체 평균(즉, 세 그룹의 평균)을 나타내는 경향이 있을 가능성이 매우 높다.

'오른쪽 그래프'는 서로 떨어진 세 개의 분포를 나타내며, 그 중 어느 것도 겹치지 않는다. 전체 평균과 그룹 평균의 차이가 클 가능성이 높다.

032918_0906_RANOVATutor1

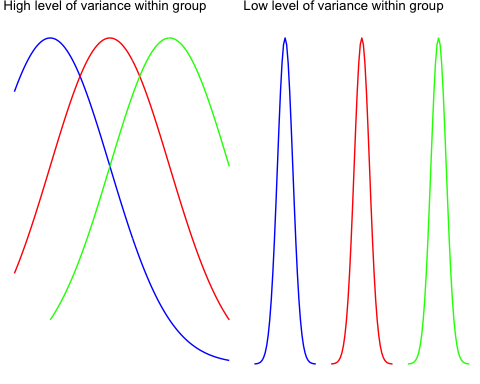
그룹 내 변동성(within group variability) 그룹 간의 차이를 고려한다. 이 편차(variation)는 개별 관측치에서 비롯된다. 일부 점들은 집합 평균과 완전히 다를 수 있다. 그룹 내 변동성은 이 효과를 파악하고 샘플링 오류를 참조한다.

그룹 내 변동성의 개념을 시각적으로 이해하려면 아래 그래프를 참조하기 바란다.

'왼쪽 부분'은 세 개의 다른 그룹의 분포를 보여준다. 각 표본의 흩어짐을 증가시켰고, 개별 분산이 크다는 것은 분명하다. F-검정이 감소할 것이고, 이는 귀무 가설을 받아들일 가능성을 의미한다.

The right part shows exactly the same samples (identical mean) but with lower variability. It leads to an increase of the F-test and tends in favor of the alternative hypothesis.

'오른쪽 부분'은 정확히 동일한 표본(같은 평균)을 보여주지만, 변동성은 더 낮다. 그것은 F-검정의 증가로 이어지고 대립 가설을 찬성하는 경향을 갖게 된다.

032918_0906_RANOVATutor2

F-통계량을 구성하기 위해 두 가지 척도를 모두 사용할 수 있다. F-통계량을 이해하는 것은 매우 직관적이다. 만약 분자(그룹 내 변동성)가 증가한다면, 그것은 그룹간 변동성이 높다는 것을 의미하며, 표본의 집단이 완전히 다른 분포로부터 도출되었을 가능성이 높은 것을 의미한다.

즉, F-통계치가 낮으면 그룹들의 평균 간에 큰 차이가 없거나 거의 차이가 없음을 의미한다.

예제 : 일원 ANOVA 검정

poison 데이터 세트를 사용하여 일원 분산 분석 테스트를 실행하기로 한다. 데이터 세트에는 48개의 행과 3개의 변수가 포함되어 있다 :

Time : 동물의 생존시간
poison : 사용된 독극물 종류: factor 수준 - 1, 2, 3
treat : 사용되는 치료 유형: factor 수준 - 1, 2, 3

ANOVA 테스트를 시작하기 전에 다음과 같이 데이터를 준비해야 한다.

1단계 : 데이터 불러오기
2단계 : 불필요한 변수 제거
3단계 : poison 변수를 서열 수준(ordered level)으로 변환


xxxxxxxxxx
# Example of One-Way ANOVA
library(dplyr)
PATH <- "https://raw.githubusercontent.com/guru99-edu/R-Programming/master/poisons.csv"
df <- read.csv(PATH) %>%
select(-X) %>% 
mutate(poison = factor(poison, ordered = TRUE))
glimpse(df)

결과 :


xxxxxxxxxx
## Observations: 48
## Variables: 3
## $ time   <dbl> 0.31, 0.45, 0.46, 0.43, 0.36, 0.29, 0.40, 0.23, 0.22, 0...
## $ poison <ord> 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 1, 1, 1, 1, 2, 2, 2...
## $ treat  <fctr> A, A, A, A, A, A, A, A, A, A, A, A, B, B, B, B, B, B, ...

우리의 목표는 다음과 같은 가정을 검정하는 것이다.

H₀ : 그룹 간 생존시간 평균에 차이가 없음
H₁ : 생존시간 평균은 적어도 한 그룹은 다르다.

즉, 기니 피기에게 독의 종류에 따라 생존 시간의 평균 사이에 통계적인 차이가 있는지 알고자 한다. (좀 잔인한 실험이네!!!)

다음과 같이 한다.

1단계: poison 변수의 형식 확인
2단계: 요약 통계량 인쇄: 빈도, 평균 및 표준 편차
3단계: 상자도표 그리기
4단계: 일원 ANOVA 검증 계산
5단계: 쌍대 t-검정 실행

단계 1) 다음과 같은 코드로 poison의 수준을 확인할 수 있다. 그것들을 mutate() 함수를 이용하여 factor 타입으로 변환하면 세 개의 문자 값을 보게 된다.


xxxxxxxxxx
# level of poison
levels(df$poison)

Output:


xxxxxxxxxx
## [1] "1" "2" "3"

Step 2) 평균과 표준 편차를 계산한다.


xxxxxxxxxx
df %>%
    group_by(poison) %>%
    summarise(
        count_poison = n(),
        mean_time = mean(time, na.rm = TRUE),
        sd_time = sd(time, na.rm = TRUE)
    )

결과 :


xxxxxxxxxx
## 
# A tibble: 3 x 4
##   poison count_poison mean_time    sd_time
##    <ord>        <int>     <dbl>      <dbl>
## 1      1           16  0.617500 0.20942779
## 2      2           16  0.544375 0.28936641
## 3      3           16  0.276250 0.06227627

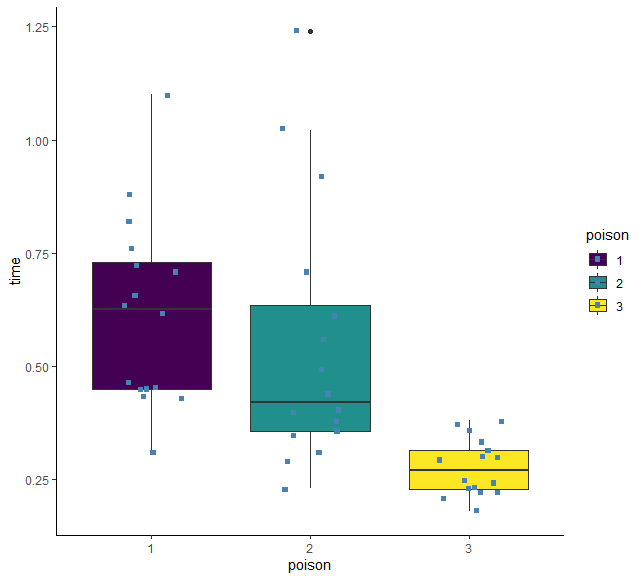
Step 3) 3단계에서는 분포 간에 차이가 있는지 그래픽으로 확인할 수 있다.

주의 : 흩어진 점(jittered dots)을 포함시킨다.


x
ggplot(df, aes(x = poison, y = time, fill = poison)) +
    geom_boxplot() +
    geom_jitter(shape = 15,
        color = "steelblue",
        position = position_jitter(0.21)) +
    theme_classic()

결과 :

1569993724310

Step 4) aov() 명령을 사용하여 일원 ANOVA 검정을 실행할 수 있다. ANOVA 검정의 기본 구문은 다음과 같다 :


xxxxxxxxxx
aov(formula, data)

인수 :

formula : 추정하고자 하는 방정식
data : 사용되는 데이터 세트

formular의 구문법은 다음과 같다 :


xxxxxxxxxx
y ~ X1 + X2 +...+ Xn      # X1 +  X2 +... refers to the independent variables
y ~ .                     # use all the remaining variables as independent variables

기니 피그 사이에 주어진 독의 종류에 따른 생존 시간에 차이가 있을까 라는 질문에 답할 수 있다.

주의 : 결과를 더 잘 확인하려면 모델을 저장하고 summary() 함수를 사용하는 것이 좋다.


xxxxxxxxxx
# one-way ANOVA test
anova_one_way <- aov(time~poison, data = df)
summary(anova_one_way)

코드 설명 :

aov(time ~ poison, data = df) : 다음의 공식을 사용하여 ANOVA 검정 실행
summary(anova_one_way) : 검정의 요약정보 출력

결과 :


xxxxxxxxxx
##             Df Sum Sq Mean Sq F value   Pr(>F)
## poison       2  1.033  0.5165   11.79 7.66e-05 ***
## Residuals   45  1.972  0.0438                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

p-값은 통상적인 임계값인 0.05보다 낮다. 당신은 "*"로 표시된 그룹 간에 통계적 차이가 있다고 말해도 된다.

쌍대 비교

일원 ANOVA 검정은 어느 그룹의 평균이 다른지 알려주지 않는다. 대신 TukeyHSD() 함수를 사용하여 Tukey 검정을 수행할 수 있다.


xxxxxxxxxx
# pairwise comparison
TukeyHSD(anova_one_way)

결과 :


x
##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = time ~ poison, data = df)
## 
## $`poison`
##          diff        lwr         upr     p adj
## 2-1 -0.073125 -0.2525046  0.10625464 0.5881654
## 3-1 -0.341250 -0.5206296 -0.16187036 0.0000971
## 3-2 -0.268125 -0.4475046 -0.08874536 0.0020924

이원 ANOVA

A two-way ANOVA test adds another group variable to the formula. It is identical to the one-way ANOVA test, though the formula changes slightly:

이원 ANOVA 검정은 공식에 다른 그룹 변수를 추가한다. 일원 ANOVA 검정과 같지만 동일하지만 공식은 약간 변한다.

y = x_1 + x_2

, 정량 변수와 범주형 변수다.

이원 ANONA 검정의 가설 :

H₀: 평균은 두 변수(즉, 요인 변수) 모두 같다.
H₁ : 평균은 두 변수 모두 다르다.

당신은 우리의 모델에 treat 변수를 추가한다. 이 변수는 기니 피그에게 주어진 치료법을 나타낸다. 당신은 기니 피그에게 주어진 poison과 treat 사이에 통계적 의존성이 존재하는지에 대해 관심이 있다.

우리는 다른 독립변수로 treat를 추가하여 코드를 수정한다.


xxxxxxxxxx
# two-way ANOVA test
anova_two_way <- aov(time~poison + treat, data = df)
summary(anova_two_way)

결과 :


xxxxxxxxxx
##             Df Sum Sq Mean Sq F value  Pr(>F)    
## poison       2 1.0330  0.5165   20.64 5.7e-07 ***
## treat        3 0.9212  0.3071   12.27 6.7e-06 ***
## Residuals   42 1.0509  0.0250                    
## ---

poison과 treat 모두 통계적으로 0과 다르다는 결론을 내릴 수 있다. 귀무 가설을 기각하고 treat나 poison을 바꾸는 것이 생존 시간에 영향을 미치고 있음을 확인할 수 있다.

요약

우리는 아래 표와 같이 검정을 요약할 수 있다 :

검정	코드	가정	p-값
일원 ANOVA	`aov(y ~ X, data = df)`	H₁: 적어도 한 그룹의 평균이 다르다.	0.05
쌍대 비교	`TukeyHSD(ANOVA summary)`		0.05
이원ANOVA	`aov(y ~ X1 + X2, data = df)`	H₁: 두 그룹의 평균이 다르다.	0.05