Chapter 7 거리와 경로(Distances and paths)
평균 경로 길이 : (방향성 그래프에 대해서는 양 방향에서) 네트워크에 있는 노드들 사이의 최단 거리의 평균 - mean_distance() 함수
mean_distance(net, directed=F)## [1] 2.058824mean_distance(net, directed=T)## [1] 2.742188또한 그래프에서 모든 최단 경로들의 길이(the length of the shortest paths)를 찾을 수 있다 : distances() 함수
distances(net) # 에지 가중치 고려## s01 s02 s03 s04 s05 s06 s07 s08 s09 s10 s11 s12 s13 s14 s15 s16 s17
## s01 0 4 2 6 1 5 3 4 3 4 3 3 9 4 7 26 8
## s02 4 0 4 8 3 7 5 6 1 5 5 5 11 6 9 28 10
## s03 2 4 0 4 1 3 1 2 3 2 1 1 7 2 5 24 6
## s04 6 8 4 0 5 1 5 6 7 6 5 3 3 6 1 22 2
## s05 1 3 1 5 0 4 2 3 2 3 2 2 8 3 6 25 7
## s06 5 7 3 1 4 0 4 5 6 5 4 2 4 5 2 21 3
## s07 3 5 1 5 2 4 0 3 4 3 2 2 8 3 6 25 7
## s08 4 6 2 6 3 5 3 0 5 4 3 3 9 4 7 26 8
## s09 3 1 3 7 2 6 4 5 0 5 4 4 10 5 8 27 9
## s10 4 5 2 6 3 5 3 4 5 0 3 3 9 4 7 26 8
## s11 3 5 1 5 2 4 2 3 4 3 0 2 8 1 6 25 7
## s12 3 5 1 3 2 2 2 3 4 3 2 0 6 3 4 23 5
## s13 9 11 7 3 8 4 8 9 10 9 8 6 0 9 4 22 1
## s14 4 6 2 6 3 5 3 4 5 4 1 3 9 0 7 26 8
## s15 7 9 5 1 6 2 6 7 8 7 6 4 4 7 0 23 3
## s16 26 28 24 22 25 21 25 26 27 26 25 23 22 26 23 0 21
## s17 8 10 6 2 7 3 7 8 9 8 7 5 1 8 3 21 0distances(net, weights=NA) # 에지 가중치 무시 ## s01 s02 s03 s04 s05 s06 s07 s08 s09 s10 s11 s12 s13 s14 s15 s16 s17
## s01 0 1 1 1 1 2 2 2 2 2 2 2 3 3 1 3 2
## s02 1 0 1 2 1 3 2 2 1 1 2 2 3 3 2 4 3
## s03 1 1 0 1 1 2 1 1 2 1 1 1 2 2 2 3 2
## s04 1 2 1 0 2 1 2 2 3 2 1 1 2 2 1 2 1
## s05 1 1 1 2 0 2 2 2 1 2 2 2 3 3 1 3 3
## s06 2 3 2 1 2 0 3 3 3 3 2 1 2 2 1 1 1
## s07 2 2 1 2 2 3 0 1 2 1 2 2 2 1 3 4 3
## s08 2 2 1 2 2 3 1 0 1 2 2 2 3 2 3 4 3
## s09 2 1 2 3 1 3 2 1 0 1 3 3 4 3 2 4 4
## s10 2 1 1 2 2 3 1 2 1 0 2 2 3 2 3 4 3
## s11 2 2 1 1 2 2 2 2 3 2 0 2 2 1 2 3 2
## s12 2 2 1 1 2 1 2 2 3 2 2 0 1 1 2 2 2
## s13 3 3 2 2 3 2 2 3 4 3 2 1 0 1 3 2 1
## s14 3 3 2 2 3 2 1 2 3 2 1 1 1 0 3 3 2
## s15 1 2 2 1 1 1 3 3 2 3 2 2 3 3 0 2 2
## s16 3 4 3 2 3 1 4 4 4 4 3 2 2 3 2 0 1
## s17 2 3 2 1 3 1 3 3 4 3 2 2 1 2 2 1 0우리가 관심을 갖는 노드나 노드 집합에 대한 거리들을 추출할 수 있다. 예를 들어, New York Times 중심에서 모든 미디어의 거리를 계산해 보자.
dist.from.NYT <- distances(net, v=V(net)[media=="NY Times"], to=V(net), weights=NA)
# 거리를 시각화하는 색 설정:
oranges <- colorRampPalette(c("dark red", "gold"))
col <- oranges(max(dist.from.NYT)+1)
col <- col[dist.from.NYT+1]
plot(net, vertex.color=col, vertex.label=dist.from.NYT, edge.arrow.size=.6,
vertex.label.color="white")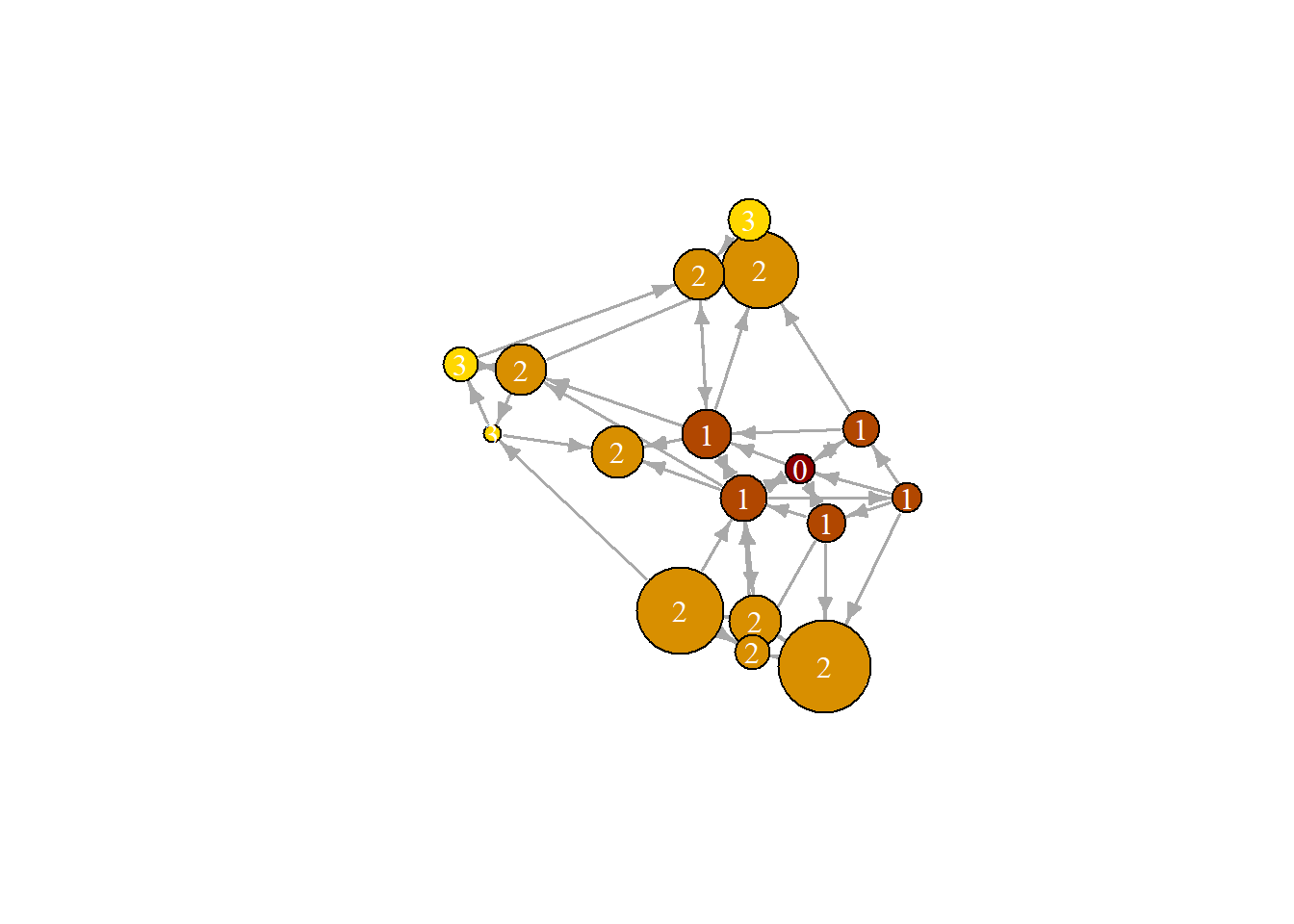
또한 특정 노드 사이의 최단 경로(shortest paths)를 찾아낼 수도 있다. shortest_paths() 함수
여기서는 MSNBC와 New York Post 사이의 최단 경로를 찾아보자.
news.path <- shortest_paths(net,
from = V(net)[media=="MSNBC"],
to = V(net)[media=="New York Post"],
output = "both") # 노드와 에지 모두
# 경로를 시각화하기 위한 에지 색 변수 생성
ecol <- rep("gray80", ecount(net))
ecol[unlist(news.path$epath)] <- "orange"
# 경로를 시각화하기 위한 에지 넓이(width) 변수 생성
ew <- rep(2, ecount(net))
ew[unlist(news.path$epath)] <- 4
# 경로를 시각화하기 위한 노드 색 변수 설정
vcol <- rep("gray40", vcount(net))
vcol[unlist(news.path$vpath)] <- "gold"
plot(net, vertex.color=vcol, edge.color=ecol,
edge.width=ew, edge.arrow.mode=0)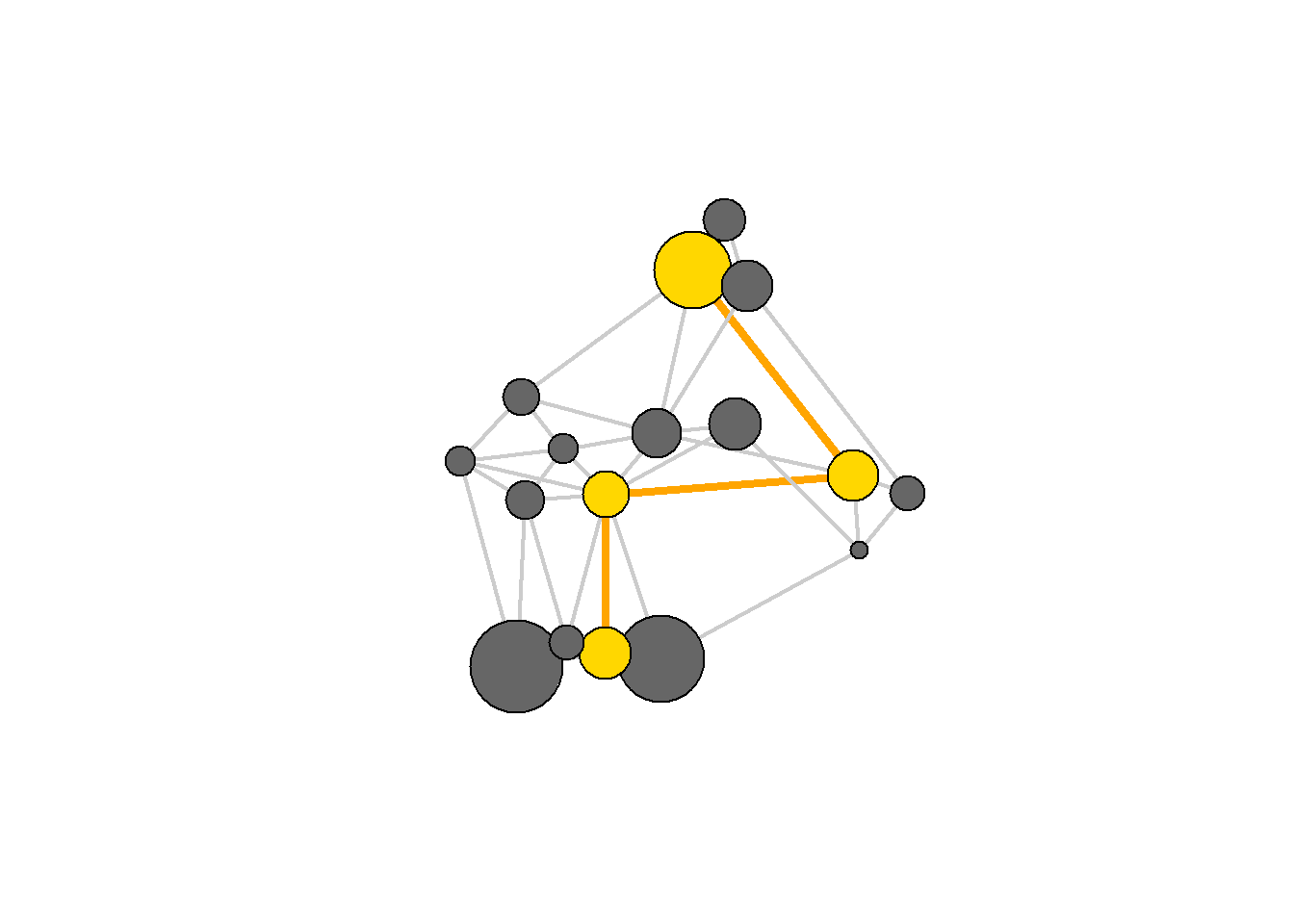
예를 들어, WSJ이라는 정점으로 들어가거나 정점에서 나오는 에지들을 확인해 보자. 단일 노드의 경우, incident() 함수를 사용하고, 복수 노드인 경우는 incident_edges() 함수를 사용한다.
inc.edges <- incident(net, V(net)[media=="Wall Street Journal"], mode="all")
# 선택된 에지를 시각화하기 위해 색 설정
ecol <- rep("gray80", ecount(net))
ecol[inc.edges] <- "orange"
vcol <- rep("grey40", vcount(net))
vcol[V(net)$media=="Wall Street Journal"] <- "gold"
plot(net, vertex.color=vcol, edge.color=ecol)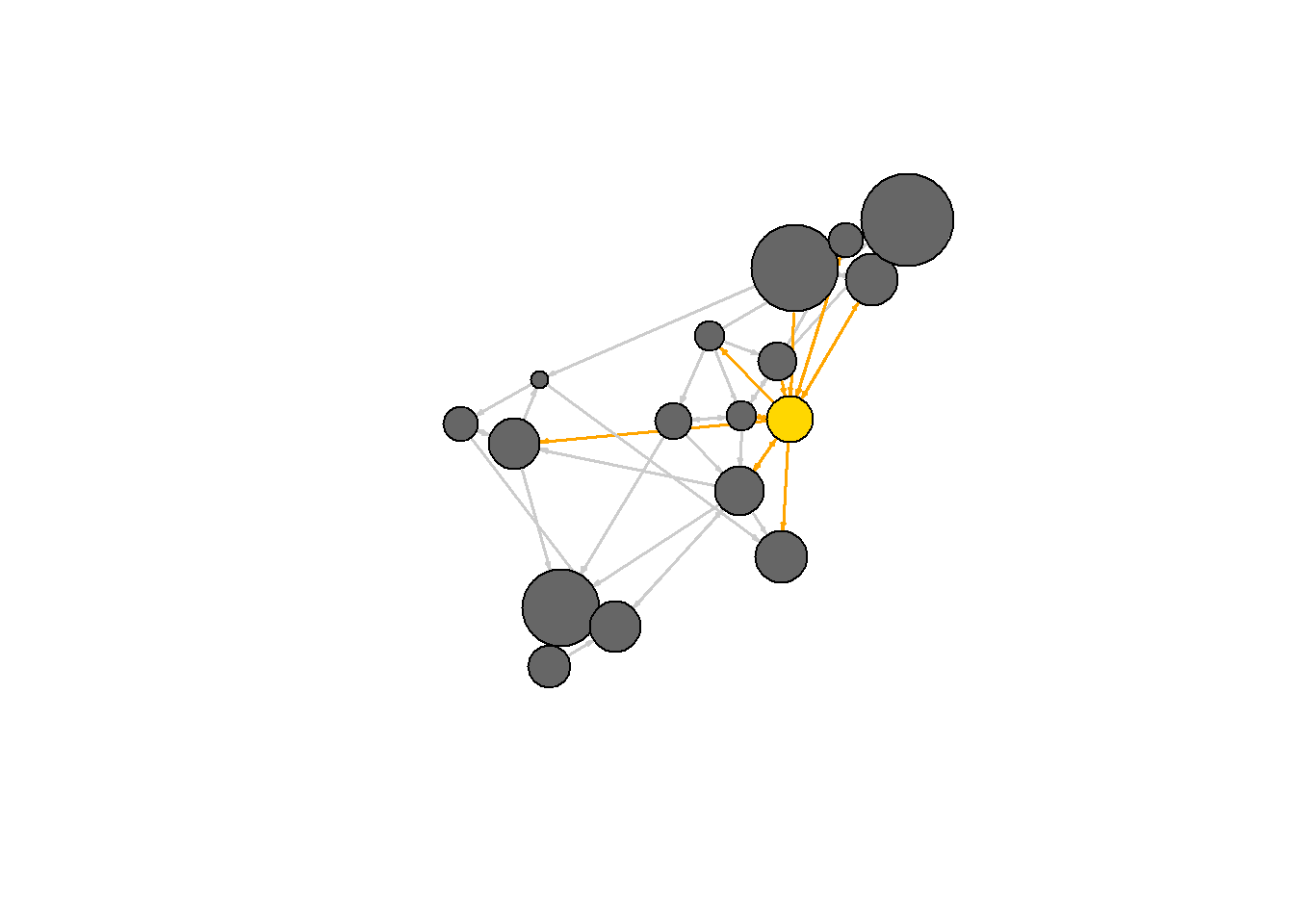
또한 WSJ라는 정점과 인접한 이웃들(neighbors)을 쉽게 식별할 수도 있다. neighbors() 함수는 관심 노드에서 한 단계 인접한 모든 노드들을 찾아준다. 복수 노드들의 이웃을 찾기 위해서는 neighbors() 대신에 adjacent_vertices() 함수를 이용한다. 한 단계 이상의 이웃 노드들을 찾기 위해서는 관심 노드(들)로 부터 떨어진 단계의 수를 order 파라미터로 설정하는 ego() 함수를 이용한다.
neigh.nodes <- neighbors(net, V(net)[media=="Wall Street Journal"], mode="out")
# 이웃들을 시각화하기 위해 색 설정
vcol[neigh.nodes] <- "#ff9d00"
plot(net, vertex.color=vcol)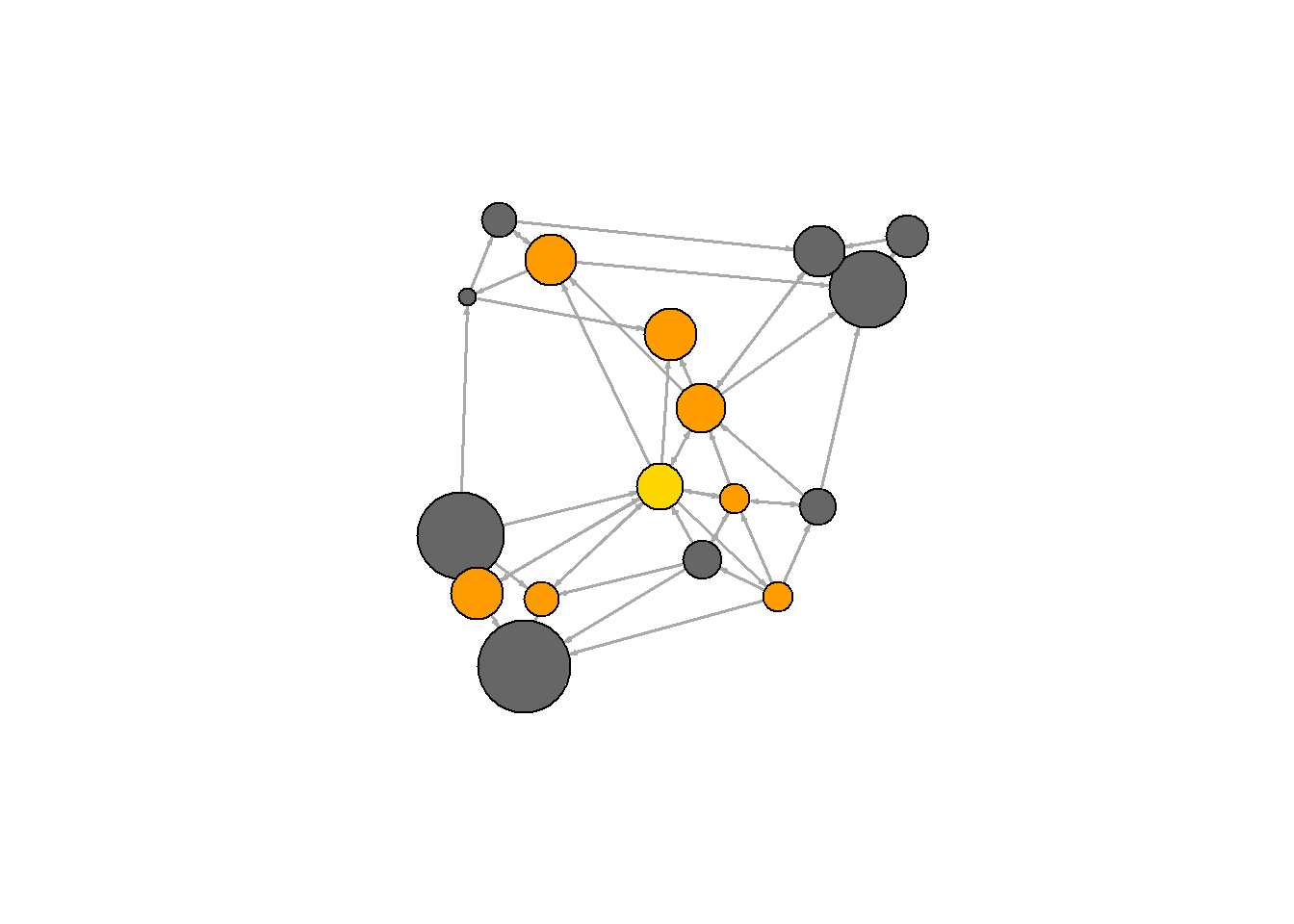
에지 순서의 색인화를 위한 특별한 연산자들 : %–%, %->%, %<-%
* E(network)[X %–% Y] : 방향은 무시하고 정점 X와 Y 집합 사이의 에지들 선택
* E(network)[X %->% Y] : 정점집합 X에서 정점 집합 Y로 향하는 모든 에지들 선택
* E(network)[X %<-% Y] : 정점집합 Y에서 정점 집합 X로 향하는 모든 에지들 선택
예를 들어, 정점의 type.label이 newpaper에서 online 출처로 향하는 모든 에지들을 선택해 보자.
E(net)[ V(net)[type.label=="Newspaper"] %->% V(net)[type.label=="Online"] ]## + 7/48 edges from d3766f8 (vertex names):
## [1] s01->s15 s03->s12 s04->s12 s04->s17 s05->s15 s06->s16 s06->s17공동 인용(Co-citation)(노드들에 대해, 얼마나 많이 서로 이름들을 공유하고 있는지를 나타냄) : cocitations() 함수 사용
cocitation(net)## s01 s02 s03 s04 s05 s06 s07 s08 s09 s10 s11 s12 s13 s14 s15 s16 s17
## s01 0 1 1 2 1 1 0 1 2 2 1 1 0 0 1 0 0
## s02 1 0 1 1 0 0 0 0 1 0 0 0 0 0 2 0 0
## s03 1 1 0 1 0 1 1 1 2 2 1 1 0 1 1 0 1
## s04 2 1 1 0 1 1 0 1 0 1 1 1 0 0 1 0 0
## s05 1 0 0 1 0 0 0 1 0 1 1 1 0 0 0 0 0
## s06 1 0 1 1 0 0 0 0 0 0 1 1 1 1 0 0 2
## s07 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0
## s08 1 0 1 1 1 0 0 0 0 2 1 1 0 1 0 0 0
## s09 2 1 2 0 0 0 1 0 0 1 0 0 0 0 1 0 0
## s10 2 0 2 1 1 0 0 2 1 0 1 1 0 1 0 0 0
## s11 1 0 1 1 1 1 0 1 0 1 0 2 1 0 0 0 1
## s12 1 0 1 1 1 1 0 1 0 1 2 0 0 0 0 0 2
## s13 0 0 0 0 0 1 0 0 0 0 1 0 0 1 0 0 0
## s14 0 0 1 0 0 1 0 1 0 1 0 0 1 0 0 0 0
## s15 1 2 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0
## s16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
## s17 0 0 1 0 0 2 0 0 0 0 1 2 0 0 0 1 0