3.3 이상치(Outlier) 처리 {#outlier}
3.3.1 표준값 Z를 이용한 이상치 확인 및 처리
outliers패키지를 이용해서 Z값(Z-score) 이상값을 결측치로 대체하는 방법이 있다.- Z-값은 통계학에서 매우 기본이 되는 값으로,z = (x-μ)/σ로 구해지는 값이다.
- 이를 통해 서로 단위나 크기가 다른 값을 모두 표준화시킬 수 있다. 따라서 표준점수, 표준값이라고도 합니다.
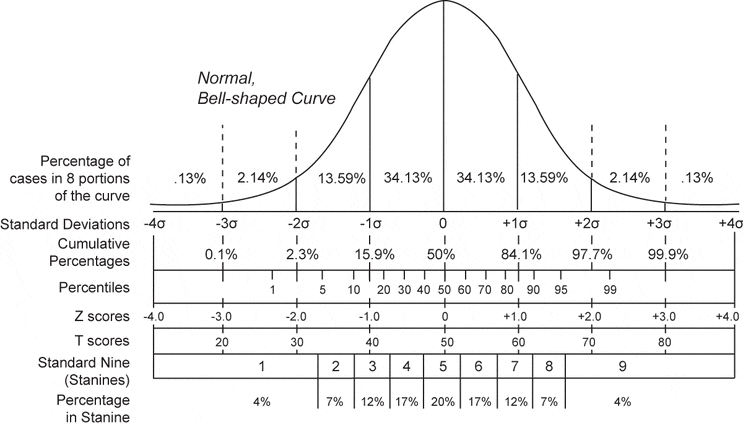
- 표준점수 0.0(=편차치 50) 이상은 전체의 50%이다.
- **표준점수의 절대값**이 1.0(=편차치 60) 이상은 전체의 31.74%이다.
- **표준점수의 절대값**이 2.0(=편차치 70) 이상은 전체의 4.56%이다.
- **표준점수의 절대값**이 3.0(=편차치 80) 이상은 전체의 0.28%이다.
- **표준점수의 절대값**이 4.0(=편차치 90) 이상은 전체의 0.006%이다.
- **표준점수의 절대값**이 5.0(=편차치 100) 이상은 전체의 0.00004%이다. Z의 절대값이 3.0 이상의 값을 갖는 것은 전체 관측치의 0.28% 정도로 매우 드물기 때문에 이 정도 범위에서 벗어나는 값은 이상치라는 의심을 지닐 수 있다.
물론 더 엄격한 기준을 제시할 수 있는데, 미 국립표준 기술 연구소 (NIST, National Institute of Standards and Technology)의 경우 4.0을 제시하고 있으며 연구자에 따라서는 3.5를 사용할 수 있다.
3.3.1.1 outliers 패키지 설치
# install.packages("outliers")
library(outliers)3.3.1.2 정규분포 데이터 세트 생성
평균 100, 표준편차 3의 정규분포를 하는 샘플 300개를 rnorm() 함수를 이용하여 데이터 세트 x1을 생성한다.
set.seed(1234)
x1 <- rnorm(300, 100, 3) # 평균 100, 표준편차 3인, 표본 300개 생성이렇게 생성된 샘플의 분포도를 그려본다.
plot(x1)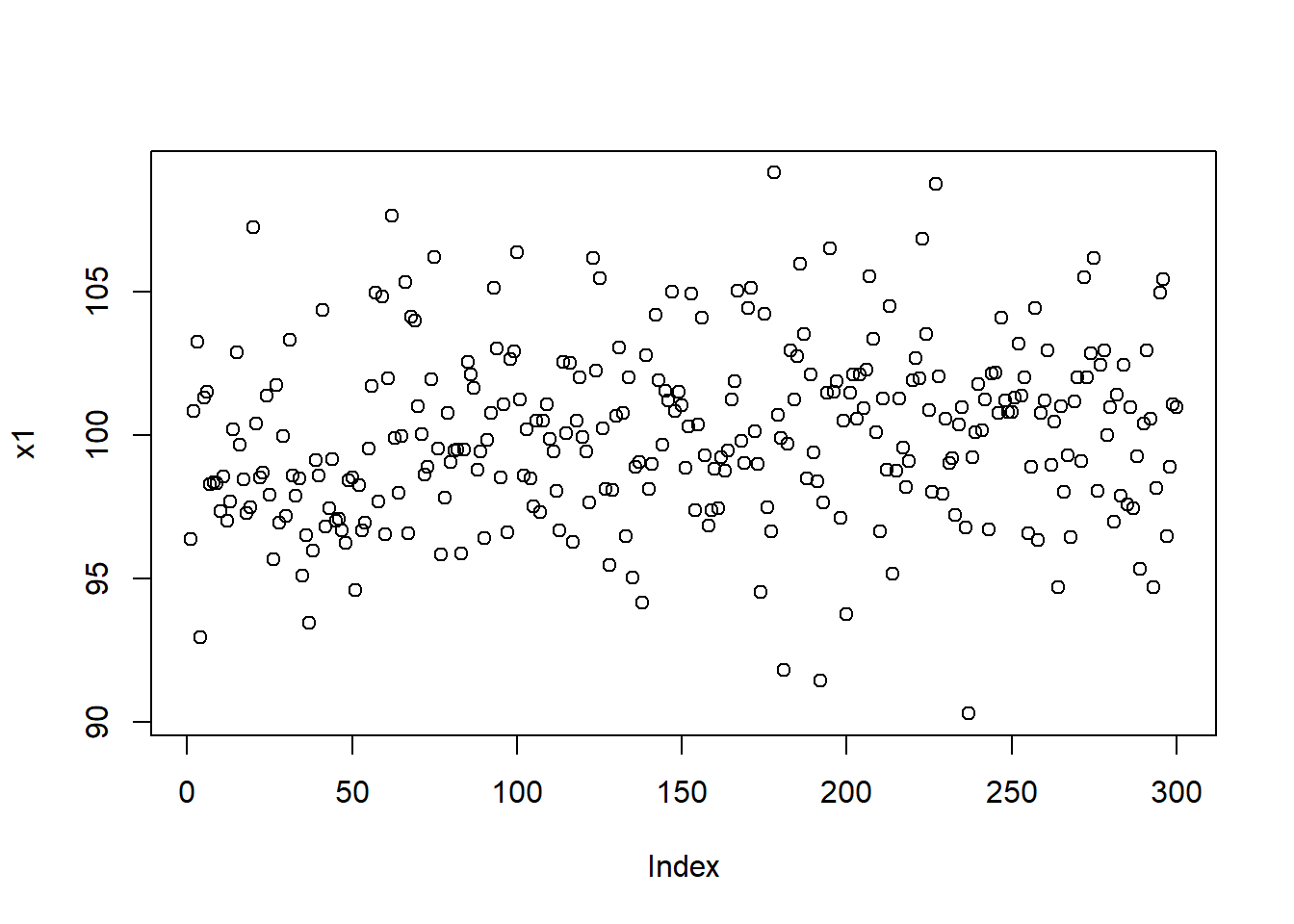
3.3.1.3 이상치의 존재유무 확인
정규분포를 따르더라도 확률적으로 Z의 절대값이 3을 넘을 수 있다. 즉, Z값이 3보다 크거나 Z값이 -3보다 작을 수 있다.
다만 이 코드에서는 쉽게 확인할 수 없으므로 outliers 패키지의 scores() 함수를 이용해서 찾아본다. (도움말은 ? scores() 참조)
Z값을 나타내는 Z라는 새로운 데이터를 생성하고, 이 Z 값의 분포도를 plot() 함수를 이용하여 그리고, Z의 절대값이 3이 되는 수평선을 그려본다.
Z <- scores(x1, type="z")
plot(Z, col = ifelse(abs(Z)>3, "red", "blue"))
abline(h = 3, col="blue")
abline(h =-3, col="blue")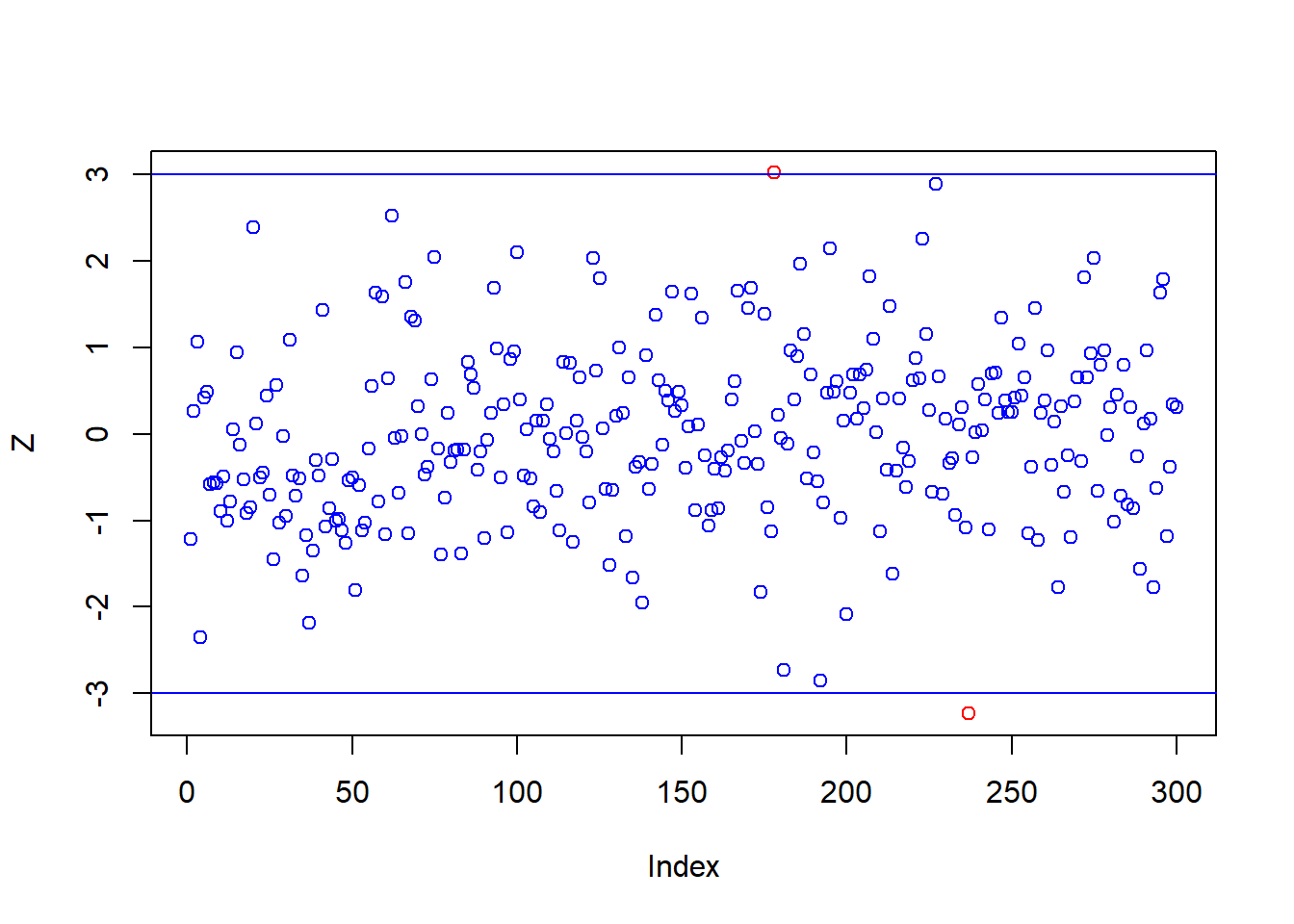 -
- scores(x1, type="z") : 데이타 x1에 대한 표준값(z)을 반환
- plot(Z, col = ifelse(abs(Z)>3, "red", "blue")) : Z의 절대값이 3보다 크면 점의 색깔을 빨간색으로, 그렇지 않으면 파란색으로 표시한다.
- abline(h = 3, col="blue") : Z 값이 3인 수평선을 그린다.
- 이 분포도에서 2개의 outlier가 존재함을 확인할 수 있다.
이 Z의 절대값 중 3을 넘는 값의 존재함을 확인하였으나 이상치의 정확한 색인 번호는 which() 함수를 이용하여 확인할 수 있다.
which(Z %in% Z[abs(Z) > 3])## [1] 178 237%in%: 벡터 내 특정 값 포함 여부 확인 연산자. 색인 번호 반환.- 178번과 237본 두 개의 데이터가 이상치.
3.3.1.4 이상치를 결측치로 대체
두 개의 이상치가 존재함을 확인하였으므로, 이제 이 이상치를 결측치 NA로 변경한다.
x1[which(Z %in% Z[abs(Z) > 3])] <- NA
x1[c(178, 237)]## [1] NA NA- 178번째 값과 237번째 값이
NA로 변경되어 있음.
또 다른 방법은 replace() 함수를 이용하여 이상치(Z>3) 조건을 만족하는 x1의 값을 결측치 NA로 변경할 수 있다.
x1 <- replace(x1, abs(Z) > 3, NA)
x1[178]## [1] NA이렇게 표준에서 크게 벗어난 값을 보다 논리적으로 해결할 수 있게 되었다.
3.3.1.5 이상치 제거 시의 주의점
원래 데이터에 너무 많은 이상치가 존재하는 경우에는 이상치 제거에 신중해야 한다.
3.3.2 수정된 표준값을 이용한 이상치 확인 및 처리
표준값을 이용하는 방법은 가장 일반적이고 간단한 접근이다
그러나, 관측값(즉 표본)의 숫자가 적은 경우 정상적인 데이터가 이상치로 처리되는 경우가 있을 수 있다.
극단적인 예를 든다면, 20명의 소득을 조사했는데, 그 가운데 특별히 빌 게이츠가 끼어 있는 경우이다. 이 경우 소득의 평균값이 수백만 달러로 올라가게 되고, 그러면 5만 달러, 10만 달러의 연봉을 받는 사람까지 이상치로 처리될 수 있는 것이다.
이렇게 평균을 내면 본래 이상치가 아닌 것도 이상치로 만들 수 있다.
이를 회피하는 가장 좋은 방법은 평균 대신 중앙값(median)을 이용하는 것이다.
집단에서 중간 위치에 있는 값(중앙값)을 기준으로 잡으면, 평균의 함정에서 벗어날 수 있다.
3.3.2.1 데이터 세트의 생성
이번에는 평균이 100이고 표준편차가 3으로 정규분포하는 샘플을 3,000개 생성한다.
set.seed(1234)
x2 <- rnorm(3000,100,3)3.3.2.2 수정된 표준값 계산
표준값의 계산에 있어서 평균값이 아닌 중앙값을 사용하는 방법에 대하여 알아본다.
outliers 패키지의 score() 함수에서 type= 인수로 mad를 지정하고 변수명은 Zm으로 한다.
여기서 mad는 median absolute deviation(MAD)로 중앙값의 절대 편차값을 의미한다.
이렇게 구해진 값은 수정된 표준값(modified Z score)라고 한다.
Zm <- scores(x2, type="mad")scores(x2, type="mad"): 데이터 x2에 대한 수정된 표준값 반환
plot() 함수를 이용하여 수정된 표준값의 분포도를 그려본다.
plot(Zm, col = ifelse(abs(Zm)>3, "red", "blue"))
abline(h = 3, col="blue")
abline(h =-3, col="blue")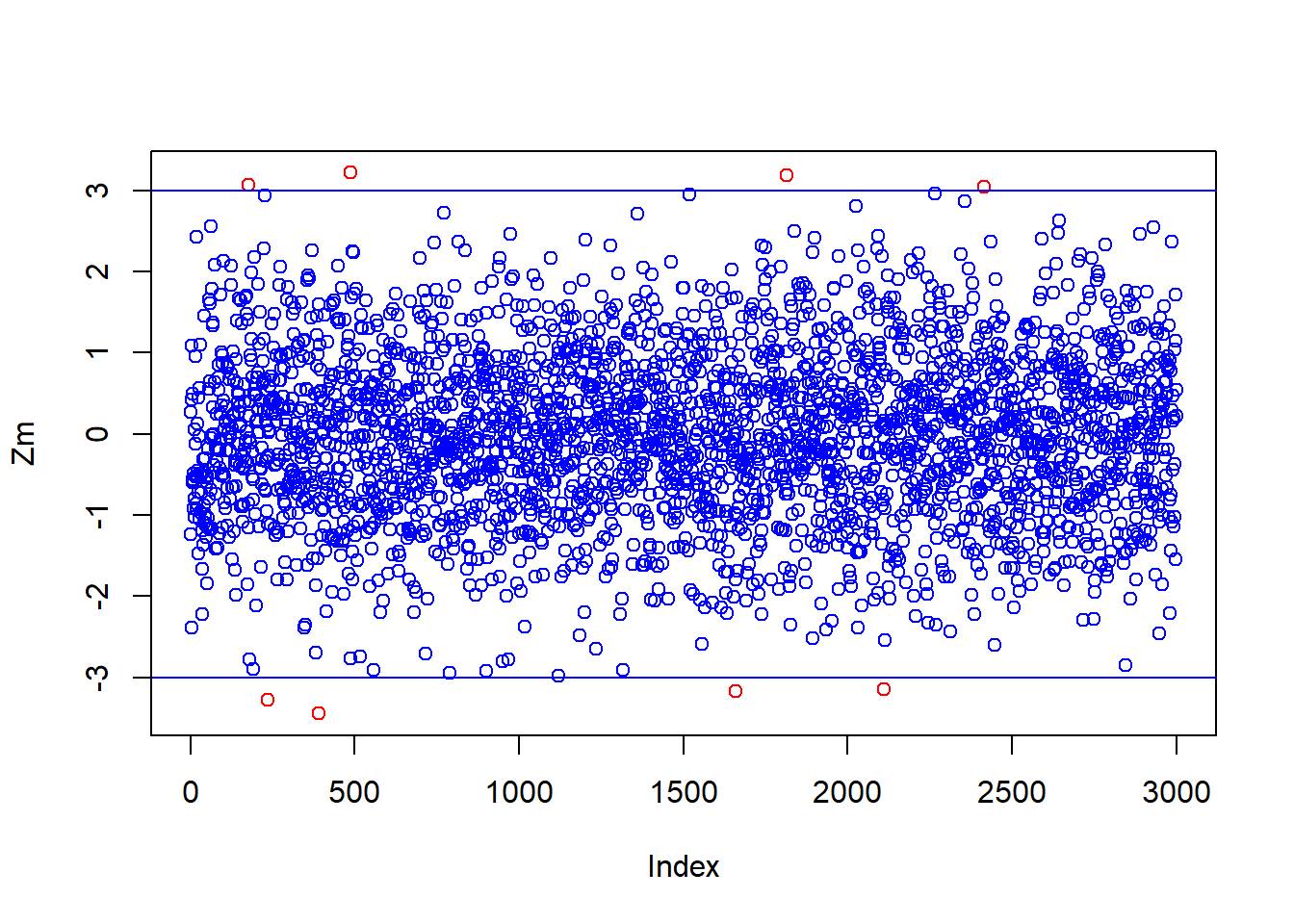
- 8개의 이상치가 있음을 확인할 수 있다.
3.3.2.3 이상치의 위치 확인
이제 수정된 표준값의 절대값이 3보다 큰 값들의 색인번호를 which() 함수를 이용하여 이상치의 위치를 확인한다.
which(abs(Zm) >3)## [1] 178 237 392 486 1660 1815 2111 2414- 총 8개의 이상치가 있다.
3.3.2.4 이상치를 결측치로 대체하기
샘플 데이터 x2의 이상치를 which() 함수를 이용하여 결측치로 대체한다
x2[which(abs(Zm) >3)] <- NA
x2[which(abs(Zm) >3)]## [1] NA NA NA NA NA NA NA NA3.3.2.5 데이터 프레임으로 데이터 확인하기
샘플 데이터 x2와 수정된 표준값 Zm을 데이터 프레임 df로 만들어 본다.
df <- data.frame(x2, Zm)
head(df)## x2 Zm
## 1 96.37880 -1.2328145
## 2 100.83229 0.2683791
## 3 103.25332 1.0844689
## 4 92.96291 -2.3842547
## 5 101.28737 0.4217810
## 6 101.51817 0.4995776subset() 함수를 이용해 수정된 표준값 Zm의 절대값이 3이상인 값들을 구해 이상치 값들의 집합인 데이터 프레임 df1을 만들어 보자.
df1 <- subset(df, abs(Zm) > 3)
df1## x2 Zm
## 178 NA 3.065834
## 237 NA -3.281692
## 392 NA -3.446436
## 486 NA 3.219680
## 1660 NA -3.168874
## 1815 NA 3.191402
## 2111 NA -3.141637
## 2414 NA 3.044304- 8개의 이상치 데이터와 수정된 표준값을 확인할 수 있다.
3.3.3 사분위수를 이용한 이상치 확인 및 처리
사분 범위(IQR: Interquartile range)에서 크게 벗어난 값을 이상치로 설정하는 방법에 대해서 살펴본다.
3.3.3.1 사분 범위를 이용한 이상치 계산식
사분 범위에서의 이상치는 다음과 같이 계산된다.
`Q3 + 1.5 * IQR`과 `Q1 - 1.5 * IQR`
여기서, Q1 : 1 사분위수
Q3 : 3 사분위수
IQR : 사분 범위3.3.3.2 사분범위 방법과 표준값 방법의 비교
사실 정규 분포를 따르더라도 표본 수가 많아지면, (Q3 + 1.5 * IQR)와 (Q1 - 1.5 * IQR)를 벗어나는 값도 같이 많아지기 때문에 그만큼 이상치로 보는 숫자가 점점 많아진다는 점도 고려해야 한다.
사분범위를 이용한 방법과 앞서 Z값 3을 기준으로 삼는 방법 간의 차이점을 우선 비교해 보면 다음의 그림과 같다.
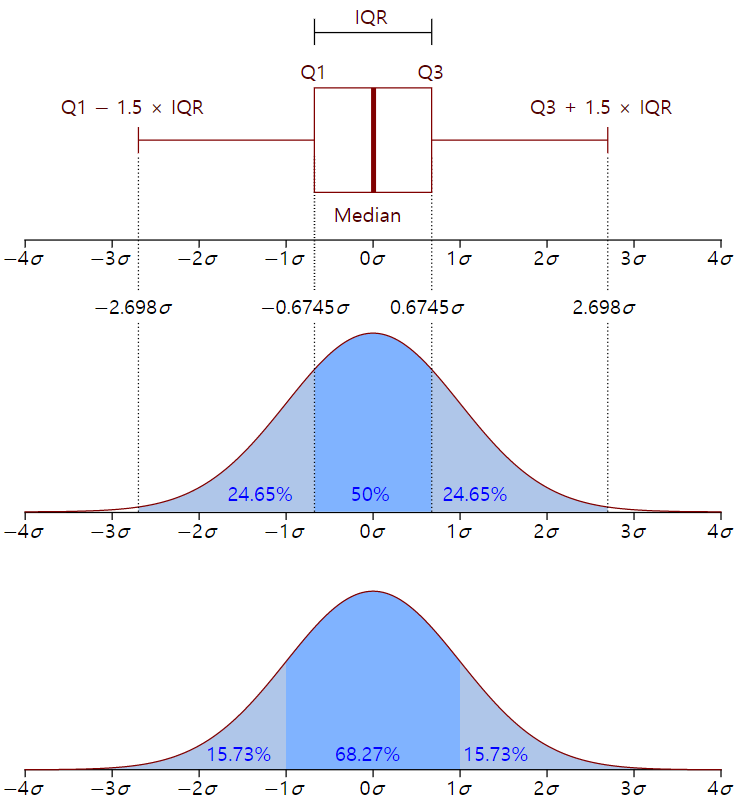
(출처 : 위키피디어)
- IQR은 4사 분위수(Q3, 75번째 백분위수)에서 2사분위수(Q1, 25번째 백분위수)을 뺀 값이다. 즉, IQR = Q3 - Q1이다.
- Q1은 표준값 -.6745 그리고 Q3는 표준값 .6745에 해당된다.
Q1 - 1.5 * IQR은 표준값 -2.698, 그리고Q3 + 1.5 * IQR은 표준값 2.698에 해당된다.
3.3.3.3 데이터 세트의 생성
여기서도 편의상 평균 100, 표준편차 3을 갖는 샘플 3천개인 데이터 세트 x3를 생성한다.
set.seed(1234)
x3 <- rnorm(3000, 100, 3)이 샘플 데이터의 분포도를 그려보자.
plot(x3)
3.3.3.4 사분범위를 이용한 이상치의 상한과 하한 계산
데이터 세트 x3에 대한 사분범위를 이용한 이상치의 계산은 다음과 같은 outlier() 함수를 생성하여 계산한다.
outlier <- function(x) {
low_Outlier <- quantile(x)[2] - 1.5 * IQR(x)
up_Outlier <- quantile(x)[4] + 1.5 * IQR(x)
return(c(low_Outlier, up_Outlier))
}
outlier(x3)## 25% 75%
## 91.9957 108.01943.3.3.5 이상치 존재 유무 확인하기
데이터 세트의 사분범위 이상치의 하한과 상한을 outlier() 함수로 계산하였으므로, 이제 이 범위를 벗어나는 데이터를 찾아본다.
lim <- outlier(x3)
which(x3 > lim[2] | x3 < lim[1]) ## [1] 178 181 192 227 237 392 486 487 517 558 771 788 901 949 967
## [16] 1121 1317 1359 1517 1660 1815 2024 2111 2264 2355 2414 2844lim <- outlier(x3):x3의 사분범위 이상치의 범위값을lim변수에 대입한다. lim[1]이 하한, lim[2]가 상한- which(x3 > lim[2] | x3 < lim[1] ) : 하한보다 작거나, 상한보다 큰 값의 위치를 확인
- 총 27개의 이상치가 확인됨
3.3.3.6 이상치를 결측치로 대체하기
이상치에 대해 which() 함수를 이용하여 결측치로 대체한다.
x3[which(x3 > lim[2] | x3 < lim[1])] <- NA
sum(is.na(x3))## [1] 27sum(is.na(x3)): 전체 데이터 중NA값의 갯수.
27개의 결측값은 앞서 예제에서보다 훨씬 많다.
대략적으로 전체의 1%가 조금 안되는 값이 이상치로 분류되어 제거된 것이다.
사실 모든 값들이 정규 분포를 따르고 제거할 필요가 없는 값이라는 점을 생각하면 좀 과도하게 제거된 것일 수도 있다.
하지만 표본의 100개 이하로 좀 작다면 무리 없이 적용할 수 있을 것이다.