1.2 그래프 분석의 예
영국의 통계학자 Francis Anscombe 가 “Graphs in Statistical Analysis”(1973년)라는 논문 (링크를 클릭하면 pdf 다운로드 가능)에서 왜 통계분석을 할 때 반드시 통계치 뿐 만 아니라 그래프 분석을 병행해야 하는지를 보여주는 데이터 예를 듭니다. (x1, y1), (x2, y2), (x3, y3), (x4, y4) 변수들로 구성된 4개 그룹이 있는데요, x1~x4, y1~y4 끼리 평균, 표준편차가 같고, (x1, y1), (x2, y2), (x3, y3), (x4, y4) 변수들 간의 상관계수와 회귀모형이 같습니다. 이정도면 같은 모집단에서 뽑은 같은 성격/특징/형태를 보이는 4개의 표본이라고 지레짐작하기 쉬운데요, 그래프를 그려보면 4개의 표본이 날라도 너무 달라서 깜짝 놀라게 됩니다.
| He later became interested in statistical computing, and stressed that *“a computer should make both calculations and graphs”*, and illustrated the importance of graphing data with four data sets now known as Anscombe’s quartet |  |
|---|---|
| * source: https://en.wikipedia.org/wiki/Frank_Anscombe |
R에 base패키지인 datasets 패키지에 ’anscombe’라는 데이터 프레임이 기본 탑재되어 있는 데이터 세트이어서 쉽게 불러다가 예시를 들어보겠습니다. str()함수로 데이터 구조를 보니 8개 변수에 11개 관측치로 구성되어 있는 데이터 프레임이고, x1, x2, x3, x4, y1, y2, y3, y4 모두 숫자형(numeric) 변수들이군요.
## Anscombe's Quartet of ‘Identical’ Simple Linear Regressions
# Four x-y datasets which have the same traditional statistical properties
# (mean, variance, correlation, regression line, etc.),
# yet are quite different.
# 데이터 구조
str(anscombe)## 'data.frame': 11 obs. of 8 variables:
## $ x1: num 10 8 13 9 11 14 6 4 12 7 ...
## $ x2: num 10 8 13 9 11 14 6 4 12 7 ...
## $ x3: num 10 8 13 9 11 14 6 4 12 7 ...
## $ x4: num 8 8 8 8 8 8 8 19 8 8 ...
## $ y1: num 8.04 6.95 7.58 8.81 8.33 ...
## $ y2: num 9.14 8.14 8.74 8.77 9.26 8.1 6.13 3.1 9.13 7.26 ...
## $ y3: num 7.46 6.77 12.74 7.11 7.81 ...
## $ y4: num 6.58 5.76 7.71 8.84 8.47 7.04 5.25 12.5 5.56 7.91 ...관측치가 11개 밖에 안되므로 모두 불러와 보면 아래와 같습니다. 이처럼 숫자만 봐서는 데이터 분포, 특성, 변수간 관계가 어떠한 지 한눈에 안들어오고 이해가 잘 안되지요?
# 데이터 View
View(anscombe)이럴 때 보통 기술 통계치을 보곤 하지요. 중심화 경향을 나타내는 평균과 퍼짐 정도를 나타내는 표준편차를 살펴보겠습니다. x1~x4 의 평균과 표준편차가 같고, y1~y4의 평균과 표준편차가 같게 나왔습니다.
# 변수별 평균, 표준편차
options(digits = 2) # 소수점 자리 설정
sapply(anscombe, mean)## x1 x2 x3 x4 y1 y2 y3 y4
## 9.0 9.0 9.0 9.0 7.5 7.5 7.5 7.5sapply(anscombe, sd)## x1 x2 x3 x4 y1 y2 y3 y4
## 3.3 3.3 3.3 3.3 2.0 2.0 2.0 2.0이번에는 (x1, y1), (x2, y2), (x3, y3), (x4, y4)변수들 간의 상관계수를 살펴보겠습니다. 4개 집단 모두 상관계수가 0.82로 동일하게 나왔습니다.
# x, y 상관계수 (x, y correlation)
attach(anscombe)
cor(x1, y1) ## [1] 0.82cor(x2, y2) ## [1] 0.82cor(x3, y3) ## [1] 0.82cor(x4, y4) ## [1] 0.82detach(anscombe) 다음으로 4개의 각 집단별로 종속변수 y, 독립변수 x 로 해서 lm() 함수를 이용하여 단순 회귀모형을 적합시켜보겠습니다.
결과는 4개 집단 모두 y = 3.0 + 0.5*x 로 나왔습니다. (y절편 3.0, 변수 x의 계수 0.5)
# Simple Linear Regrassions by 4 groups `
attach(anscombe)
# The following objects are masked from anscombe (pos = 3):
# x1, x2, x3, x4, y1, y2, y3, y4 `
lm(y1 ~ x1)##
## Call:
## lm(formula = y1 ~ x1)
##
## Coefficients:
## (Intercept) x1
## 3.0 0.5lm(y2 ~ x2)##
## Call:
## lm(formula = y2 ~ x2)
##
## Coefficients:
## (Intercept) x2
## 3.0 0.5lm(y3 ~ x3)##
## Call:
## lm(formula = y3 ~ x3)
##
## Coefficients:
## (Intercept) x3
## 3.0 0.5lm(y4 ~ x4)##
## Call:
## lm(formula = y4 ~ x4)
##
## Coefficients:
## (Intercept) x4
## 3.0 0.5위에 살펴본 바를 종합해 보면,
4개 집단의
x변수들의 평균, 표준편차가 같고,y변수들의 평균, 표준편차가 같습니다.4개 집단의
x변수와y변수들 간의 상관계수가 동일합니다.4개 집단의
x독립변수와y종속변수간 단순회귀모형 적합결과x변수 계수와y절편 값이 같은 동일 모델로 적합되었습니다.
이쯤되면 4개 집단의 x, y 변수 데이트들이 동일한 모집단에서 랜덤하게 추출된 동일한 형태/분포/특성을 지닌 데이터라고 믿어도 되지않겠습니까?
그런데, 그게 아닙니다.
아래의 4개 그룹별 x변수, y변수 산포도를 살펴보시지요.
# Scatter Plot & Simple Linear Regression Line
par(mfrow = c(2,2)) # 2 x 2 layout
attach(anscombe) ## The following objects are masked from anscombe (pos = 3):
##
## x1, x2, x3, x4, y1, y2, y3, y4# The following objects are masked from anscombe (pos = 3): x1, x2, x3, x4, y1, y2, y3, y4
plot(x1, y1); abline(lm(y1~x1), col = "blue", lty = 3)
plot(x2, y2); abline(lm(y2~x2), col = "blue", lty = 3)
plot(x3, y3); abline(lm(y3~x3), col = "blue", lty = 3)
plot(x4, y4); abline(lm(y4~x4), col = "blue", lty = 3) 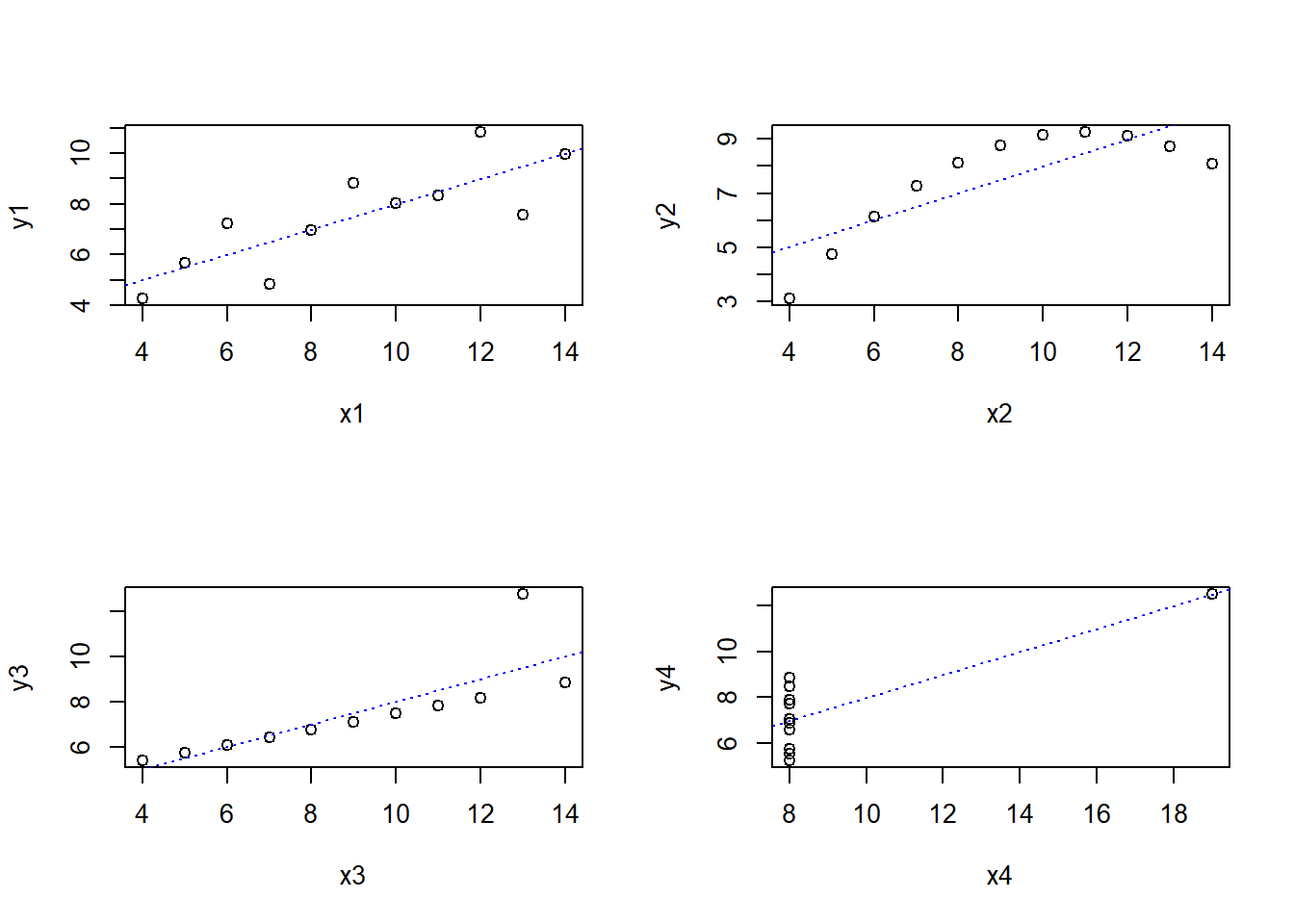
Figure 1.1: anscombe 데이터 세트의 산포도 비교
detach(anscombe)그래프를 그려서 눈으로 보니 4개 집단이 다르지요? 통계치들은 이 4개의 집단이 같다고 말하고 있지만, 그래프는 이 4개 집단이 다르다고 말하고 있습니다. 이래서 서양 표현에 “One Look Is Worth A Thousand Words” 말이 있는 거지요.